Practicing with a variety of Free NCLEX Questions exposes students to different question formats, such as multiple-choice and select-all-that-apply.
NCLEX Dosage Calculations Questions - NCLEX Questions on Dosage Calculations
Dosage Calculations NCLEX Questions Test Strategies
- Route: How the medicine is entering the body (IV. Oral, Topically)
- Medication: It’s the actual compound that is completing the effect
- Dose: The amount of medicine/compound that is being administered.
- Desired dose: dosage that the health care provider prescribed
- Available dose: the dosage strength as stated on the medication label
Metric Table:
- 1,000 Micrograms (mcg) = 1 milligram(mg)
- 1,000 milligram(mg) = 1 gram(gm)
- 1,000 (gm) = 1 kilogram(kg)
- 1 kilogram = 2.2 pound(lbs)
- 30 milliliters(ml) = 1 ounce(oz)
- 1 milliliter (ml) = 1 cubic centimeter(cc)
- 1,000 milliliters(ml) = 1 liter(L)
- 1 teaspoonltsp) = milliliters(ml)
- 3 teaspoon(tsp) = 1 tablespoon (Tbsp)
- 1 tablespoon(Tbsp) = 15 milliliters(ml)
- 2 tablespoon(Tbsp) = 1 ounce(oz)
1. Oral medicine: Solid(tablets or capsule)
No. of tablets = (Desired/Available) x tablet(ined level)
2. Oral/Parenteral Meds: Liquid form
(Desired dose/stock dose) x Dilution ( meds level)
3. IVF Rate: ml/hr = {total vol (ml) x gtt factor (15)} / no. of hours gtts/min
= vol in cc x gtt factor/ no. of hrs x 60 mins
4. Infusion Time = Total vol to infuse in ml/milliliters per hour being infused
5. Working with pediatric dose:
You can calculate a pediatric dose by dividing the child’s body surface area (BSA) by the average adult BSA (1.73 m2 ) and multiplying that number by the average adult dose of the drug.
PEDIATRIC DOSE = (BSA in m2 /Average adult BSA (1.73 m2)) x Average adult dose
Pediatric dose = Child’s body weight in kg x Required number of mg of the drug per kg.
Other important formulae:
1.Basic formula:
Dosage = (Desired Dose/ Available Dose) x Route Conversion Factor
This formula is used to calculate the amount of medication that should be administered to the patient based on the available dose and the desired dose.
2. IV rate calculation formula:
IV Rate (ml/hr) = Total Volume (ml) ÷ Time (hr)
This formula is used to calculate the infusion rate for intravenous medications, such as fluids or medications administered through a drip.
3. Pediatric dosage calculation formula:
Dosage = (Child's Weight in kg x Desired Dose) ÷ Average Adult Dose
This formula is used to calculate the appropriate dose of medication for pediatric patients based on their weight.
4. Reconstitution formula:
Dose per ml = Total amount of medication needed ÷ Total volume of diluent
This formula is used to calculate the concentration of a medication after it has been mixed with a diluent.
5. Body surface area formula:
BSA = √(Height (cm) x Weight (kg) ÷ 3600)
This formula is used to calculate the body surface area of a patient, which is important when determining medication dosages or radiation doses.
6. Flow rate calculation formula:
Flow Rate (drops per minute) = Volume (ml) x Drop Factor ÷ P Time (min)
This formula is used to calculate the rate at which an IV solution should be administered in drops per minute, based on the drop factor of the tubing.
7. Maintenance fluid calculation formula:
Maintenance Fluid (ml/hr) = Weight (kg) x 4
This formula is used to calculate the hourly rate of fluids that should be administered to a patient to maintain hydration.
8. Titration formula:
Titration = (Desired Dose ÷ Concentration) x Volume This formula is used to calculate the amount of medication needed to achieve a desired concentration, based on the volume of the medication being administered.
9. Dilution formula:
Dilution Factor = Volume of Stock Solution ÷ Volume of Diluent
This formula is used to calculate the dilution factor needed to achieve a desired concentration of a medication.
10. Adjusted body weight formula:
Adjusted Body Weight (ABW) = Ideal Body Weight (IBW) + 0.4 (Actual Weight - IBW)
This formula is used to calculate the appropriate medication dosage for overweight or obese patients, as their actual weight may not accurately reflect their body composition.
11. Alligation formula:
Alligation = (Strength of Solution A x Quantity of Solution A) + (Strength of Solution B x Quantity of Solution B) ÷ Total Quantity of Solution
This formula is used to calculate the concentration of a medication solution w'hen two or more solutions with different strengths are mixed together.
12. Drip rate calculation formula:
Drip Rate (drops per minute) = Total Volume (ml) x Drop Factor ÷ Total Time (min)
This formula is used to calculate the drip rate for medications or fluids that are administered over a specific period of time.
Remember to practice these formulae regularly and to understand the units of measurement used in medication administration. Being able to accurately calculate medication dosages is an important part of providing safe and effective patient care as a nurse.
Dosage Calculations NCLEX Practice Questions
Question 1.
A 40-year-old female patient with a height of 5'6" and an actual weight of 200 pounds is prescribed a medication with a dosage based on her adjusted body weight (ABW).
What is the correct value to fill in the blank below to calculate the patient's ABW?
(a) 160 pounds
(b) 180 pounds
(c) 200 pounds
(d) 220 pounds
Answer:
(b) 180 pounds
Explanation:
To calculate the patient's ABW using the formula, we first need to determine her Ideal Body Weight (IBW) based on her height. One commonly used formula for IBW is:
- For women: 45.5 kg + 2.3 kg for each inch over 5 feet
- For men: 50 kg + 2.3 kg for each inch over 5 feet
Converting the patient's height of 5'6" to inches, we get 66 inches.
Using the formula for women, we can calculate her IBW as:
IBW = 45.5 kg + 2.3 kg/inch x (66 inches - 60 inches)
IBW = 45.5 kg + 13.8 kg IBW = 59.3 kg IBW = 130.9 pounds (rounded to nearest tenth)
Now that we have the patient's IBW, wc can use the formula to calculate her ABW:
ABW = IBW + 0.4 (Actual Weight - IBW)
ABW = 130.9 pounds + 0.4 (200 pounds - 130.9 pounds)
ABW = 130.9 pounds + 28.4 pounds ABW = 159.3 pounds
Therefore, the correct answer is (b) 180 pounds. Option (a) 160 pounds is incorrect as it is the patient's IBW, not her ABW. Option (c) 200 pounds is the patient's actual weight and option (d) 220 pounds is an incorrect calculation, possibly mistakingly adding 0.4 to the actual weight instead of subtracting the IBW.
Question 2.
A patient is prescribed to receive 1,000 mL of 0.9% sodium chloride solution over 4 hours. The drop factor of the tubing is 15 drops per mL. What is the flow rate in drops per minute that the IV solution should be administered at?
(a) 60 drops per minute
(b) 30 drops per minute
(c) 20 drops per minute
(d) 15 drops per minute
Answer:
(b) 30 drops per minute
Explanation:
- Using the given formula, we can calculate the flow rate in drops per minute.
- Flow' Rate = Volume x Drop Factor v ÷ Time
- Substituting the given values, we get:
- Flow Rate = 1000 x 15 v ÷ (4 x 60)
- Flow Rate = 3750 ÷ 240
- Flow Rate = 15.625
Therefore, the flow' rate in drops per minute should be 15.625. However, since the drop rate has to be a w'hole number, we round off the value to the nearest whole number, which is 16. Hence, Option (a) can be eliminated as it is not closest to the calculated flow rate.
Option (d) can also be eliminated as it is equal to the drop factor, which is not the correct answer. Option (c) can be eliminated as it is not closer to the calculated flow rate compared to option (b). Therefore, the correct answer is option B, which is 30 drops per minute, the closest whole number to the calculated flow rate of 15.625.
Question 3.
A patient is prescribed 500 ml of normal saline to be infused over 4 hours. What is the appropriate IV rate (ml/hr) for this patient?
(a) 200 ml/hr
(b) 125 ml/hr
(c) 100 ml/hr
(d) 75 ml/hr
Answer:
(b) 125 ml/hr
Explanation:
To determine the appropriate IV rate for this patient, we need to use the formula:
- IV Rate (ml/hr) = Total Volume (ml) ÷ Time (hr).
- Total volume = 500 ml Time = 4 hours
- So, IV rate = 500 ÷ 4 = 125 ml/hr.
- Therefore, the correct answer is option (b) 125 ml/hr.
Option (a) 200 ml/hr is incorrect because it would deliver the entire volume too quickly, which could lead to adverse effects, such as fluid overload or electrolyte imbalances. Option (c) 100 ml/hr is incorrect because it would not deliver the entire volume within the prescribed time of 4 hours.
Option (d) 75 ml/hr is incorrect because it would also not deliver the entire volume within the prescribed time of 4 hours. In summary, the correct IV rate for this patient is 125 ml/hr, based on the given formula, and it is important to follow the prescribed rate to ensure the safe and effective administration of the medication.
Question 4.
A patient requires a dose of 250mg of medication. The medication is available in a 5mL vial, and the instructions state that the medication should be mixed with 10mL of diluent. What is the dose per mL of the medication?
(a) 25mg/niL
(b) 50mg/mL
(c) 100mg/mL
(d) 200mg/mL
Answer:
(b) 50mg/mL
Explanation:
The formula to calculate the dose per mL of a medication after it has been mixed with a diluent is:
Dose per mL = Total amount of medication needed ÷ Total volume of diluent
In this case, the total amount of medication needed is 250mg, and the total volume of diluent is 10mL.
Therefore:
Dose per mL = 250mg ÷ 10mL = 25mg/mL
However, this is not the final answer, as the medication is available in a 5mL vial. To calculate the dose per mL of the medication, we need to divide the total amount of medication by the total volume of the mixture (medication + diluent).
Total volume of the mixture = Total volume of medication + Total volume of diluent
= 5mL + lOmL = 15mL
Therefore:
Dose per mL = Total amount of medication needed ÷ Total volume of the mixture
= 250mg ÷ 15mL = 50mg/mL
Therefore:
Option (b) is the correct answer. Option (a) is incorrect, as it only takes into account the total volume of diluent, and not the total volume of the mixture.
Option (c) is incorrect, as it assumes that the total volume of medication and diluent is equal. Option (d) is incorrect, as it assumes that the total amount of medication needed is equal to the total volume of the vial, which is not the case.
Question 5.
A 6-year-old child with a weight of 20kg needs a medication with a desired dose of 30mg. The average adult dose is 60mg. What is the pediatric dosage using the pediatric dosage calculation formula?
(a) 5mg
(b) 10mg
(c) 15mg
(d) 20mg
Answer:
(b) 10mg
Explanation:
Using the pediatric dosage calculation formula:
- Dosage = (Child's Weight in kg x Desired Dose) = Average Adult Dose
- We can plug in the values given in the case study:
- Dosage = (20kg x 30mg) ÷ 60mg Dosage = 600 ÷ 60 Dosage = 10mg
Therefore, the correct pediatric dosage is 10mg.
Option (a) 5mg is incorrect because it does not take into account the child's weight and uses a lower dosage. Option (c) 15mg is incorrect because it uses a higher dosage and does not take into account the child's weight. Option (d) 20mg is incorrect because it uses a higher dosage and does not take into account the child's weight.
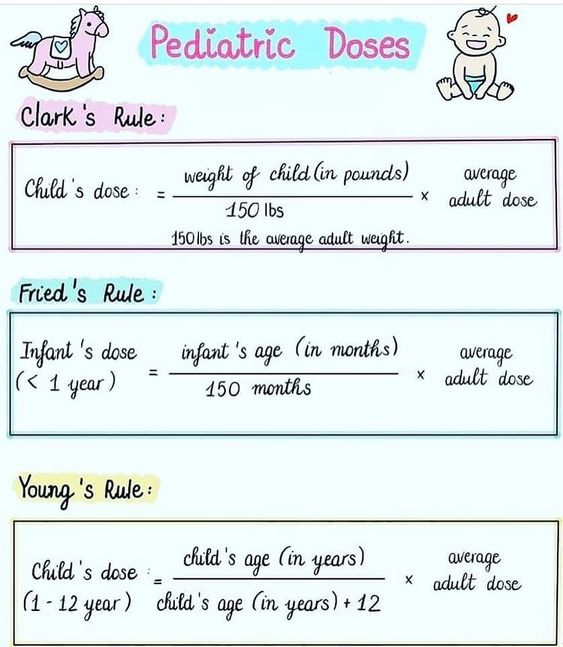
Question 6.
A 6-year-old child with a BSA of 0.75 m2 needs a medication that has an average adult dose of 500mg. What would be the pediatric dose for this child using the pediatric dosage calculation formula?
(a) 205 mg
(b) 388 mg
(c) 547 mg
(d) 697 mg
Answer:
(b) 388 mg
Explanation:
Using the pediatric dosage calculation formula given above:
- Pediatric dose = (BSA in m2 / Average adult BSA (1.73 m2)) x Average adult dose
- We are given that the child's BSA is 0.75 m2, and the average adult dose of the drug is 500mg. So, substituting the values in the formula:
- Pediatric dose = (0.75 m2 / 1.73 m2) x 500 mg
- Pediatric dose = 0.433 x 500 mg Pediatric dose = 216.5 mg (rounded to the nearest tenth)
Therefore, the correct answer would be option (b) 388 mg as it is the closest value to 216.5 mg provided in the options. Option (a) 205 mg is too low and Option (c) 547 mg and Option (d) 697 mg are too high. It is important to note that pediatric dosages should always be double-checked and verified by a licensed healthcare provider to ensure accuracy and safety.
Question 7.
If a patient is prescribed 500 meg of a medication, what is the equivalent in milligrams?
(a) 0.5 mg
(b) 5 mg
(c) 50 mg
(d) 500 mg
Answer:
(a) 0.5 mg
Explanation:
From the given formula, we know that 1,000 micrograms (meg) is equal to 1 milligram (mg). Therefore, to convert 500 meg to mg. we need to divide 500 by 1.000.
500 meg ÷ 1.000 = 0.5 mg
- 1,000 Micrograms (mcg) = 1 milligram(mg)
- 1.000 milligram(mg) = 1 gram(gm)
- 1,000 (gm) = 1 kilogram(kg)
- 1 kilogram = 2.2 pound(lbs)
- 30 milliliters(ml) = 1 ounce(oz)
- 1 milliliter (ml) = 1 cubic centimeter(cc)
- 1.000 milliliters(ml) = 1 liter(L)
- 1 teaspoon(tsp) = 5 milliliters(ml)
- 3 tcaspoon(tsp) = 1 tablespoon (Tbsp)
- 1 tablespoon(Tbsp) = 15 milliliters(ml)
- 2 tablespoon(Tbsp) = 1 ounce(oz)
So. the correct answer is option (a) 0.5 mg. Option (b) 5 mg is incorrect as it is 10 times higher than the correct answer. Option (c) 50 mg is incorrect as it is 100 times higher than the correct answer. Option (d) 500 mg is incorrect as it is 1,000 times higher than the correct answer.
Question 8.
The doctor orders for an oral suspension 75 mg by mouth every' 6 hours pm. You’re dispensed with a bottle that labels 10 mg/ml? How many teaspoons will you administer per dose?
(a) 0.25 teaspoons
(b) 1.5 teaspoons
(c) 2.5 teaspoons
(d) 7.5 teaspoons
Answer:
(b) 1.5 teaspoons
Explanation:
We are given that the doctor has ordered 75 mg every 6 hours. The bottle of oral suspension is labeled 10 mg/ml. This means that there are 10 milligrams of medication in every milliliter of the oral suspension. To calculate how many milliliters we need to administer for a dose of 75 mg. we need to divide the dose by the concentration of the oral suspension:
75 mg / 10 mg/'ml = 7.5 ml
Now we need to convert milliliters to teaspoons. We know that 1 teaspoon equals 5 milliliters, so:
7.5 ml / 5 rnl/tsp = 1.5 teaspoons
Therefore, the correct answer is (b). 1.5 teaspoons. Option (a), 0.25 teaspoons, is too small and does not take into account the concentration of the oral suspension. Option (c), 2.5 teaspoons, is too high and would result in overdosing the patient. Option (d), 7.5 teaspoons, is the total amount of oral suspension needed for one day, but it does not provide information about the dosage for a single administration.
Question 9.
The patient is ordered 40,000 units of heparin to be given SC everyday. Heparin is available in a 5,000 unit per 0.5 ml concentration. How much of the medicine should patient take? (Parenteral)
Question 9 How many milliliters of the heparin solution should the patient take?
(a) 2 ml
(b) 3 ml
(c) 4 ml
(d) 5 ml
Answer:
(c) 4 ml
Explanation:
To determine how many milliliters of the heparin solution the patient should take, w'e need to first calculate how many units of heparin are in each milliliter of the solution.
We are given that the heparin concentration is 5,000 units per 0.5 ml.
To convert this concentration to units per milliliter, we can use the following equation:
- 5.0 units/0.5 ml = 10,000 units/ml
- This means that each milliliter of the heparin solution contains
- 10.0 units of heparin.
- Next, w'e need to calculate how many milliliters of the solution the patient should take to receive a dose of 40,000 units. We can use the following equation:
- 40.0 units/10,000 units/ml = 4 ml
Therefore, the patient should take 4 milliliters of the heparin solution every day.
Option (a) 2 ml, is too low and would result in underdosing the patient. Option (b) 3 ml, is also too low' and does not provide the full 400 units of heparin needed. Option (d) 5 ml, is too high and would result in overdosing the patient. Therefore, the correct answer is (c) 4ml.
Question 10.
The doctor orders to infuse 1 liter of Normal saline at 200 ml/hr. You start the infusion at 06:45. At what time will the infusion be complete? (IV infusion time)
Question 10 What is the completion time for the IV infusion?
(a) 09:45
(b) 10:45
(c) 11:45
(d) 12:45
Answer:
(c) 11:45
Explanation:
To determine the completion time for the IV infusion, we need to calculate the infusion time using the formula:
- Infusion time = Volume to be infused/Infusion rate
- The volume to be infused is 1 liter, which is equivalent to 1000 ml.
- The infusion rate is 200 ml/hr.
- Substituting these values in the formula, we get:
- Infusion time = 1000 ml/200 ml/hr = 5 hours
This means that the infusion will take 5 hours to complete.
If the infusion was started at 06:45, we can add 5 hours to the start time to determine the completion time:
06:45 + 5 hours = 11:45
Therefore, the correct answer is (c) 11:45. Option (a), 09:45, is too early and does not account for the full 5 hours of infusion time. Option (b), 10:45. is also too early and would only account for 4 hours of infusion time. Option (d), 12:45, is too late and would add an extra hour to the infusion time. Therefore, the correct answer is (c) 11:45.
Also Read:
